Ramanujan’s construction for almost squaring the circle

I have ambivalent feelings about Pi Day. Certainly, anything that gets people talking about mathematics is broadly a Good Thing. And clearly a lot of people have tremendous fun, and really enter into the spirit of things, and jolly good for them. But, says a curmudgeonly voice in my head, it’s a little bit contrived. If you use base ten to represent numbers, and if you use the American month-then-day convention to represent dates, then the 14th of March gives actually a pretty rough approximation to the value of pi. (On the other hand, if you use the day-then-month ordering, the 22nd of July yields a more accurate approximation.) But this year, the sequence you get is 3/14/15, which is better than usual, especially if you happened to be looking at your clock at 9:26:53 precisely.
(I wasn’t – we went on holiday to the Peak District for the weekend, so at the numerologically significant second I was helping install a 14-month-old child into a car seat, ready to head off into one of the more scenic bits of Derbyshire for a couple of days.)
Anyway, the Aperiodical had a competition to find interesting methods of approximating pi. This looked great fun, but I totally failed to get around to doing anything about it. Many others were, as usual, better organised and motivated than me, and a list of some of their attempts can be found here.
But earlier today, in Ian Stewart‘s very readable textbook on Galois Theory, I found a nice ruler-and-compass construction, due to Ramanujan, of an approximate solution of the age-old, impossible problem of squaring the circle. This evening, I gave it a go with a moderately sharp HB pencil, a 30cm ruler, a pad of graph paper, and some compasses that were originally part of a geometry set and pencil case I got in the mid-1980s for opening a “Griffin Savers” account at the local branch of the Midland Bank (long since amalgamated into international tax-evasion facilitators HSBC).
And this is the result.

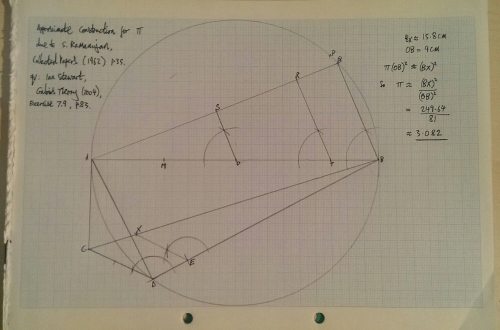
The construction is as follows: First draw a circle with centre O, and let AB be a diameter. Now M is halfway along OA and T is 2/3 along OB. P is vertically above T, and then the length BQ is equal to that of TP. TR and OS are parallel to BQ, the length of AD is equal to that of AS, and then draw AC tangent to the circle with the same length as RS. Now mark E so that BE is the same length as BM, and mark X so that EX is parallel to CD.
Once you’ve done all that, says Ramanujan, the square with side BX should be very nearly equal to the area of the circle you first thought of.
So I did all this, very carefully measured BX (~15.8cm) and OB (9 cm), and got a value of about 3.082 for pi, which isn’t that far off the correct value. With a sharper pencil and a larger piece of paper, I reckon I could probably have got a bit closer to the correct answer. I need to think further about why this construction works, and I might even get around to writing more if I figure it out.
(Also, go and visit Derbyshire sometime, because it’s very pretty.)